Python PyCrypto: Generate RSA Keys Example.py. BUT IT DOESN'T WORK WITH THE PRIVATE KEY, JUST RETURNS 0B. This comment has been minimized. Sign in to view. A Bitcoin python library for private + public keys, addresses, transactions, & RPC - blockstack/pybitcoin.

• Python Generate Bitcoin Address From Private Key
• Python Generate Private Key Bitcoin Online
• Python Generate Private Key Bitcoin Account
• Python Generate Public Key From Private Key Bitcoin

In the previous article, we looked at different methods to generate a private key. Whatever method you choose, you’ll end up with 32 bytes of data. Here’s the one that we got at the end of that article:

60cf347dbc59d31c1358c8e5cf5e45b822ab85b79cb32a9f3d98184779a9efc2

Python Generate Bitcoin Address From Private Key

We’ll use this private key throughout the article to derive both a public key and the address for the Bitcoin wallet.

What we want to do is to apply a series of conversions to the private key to get a public key and then a wallet address. Most of these conversions are called hash functions. These hash functions are one-way conversions that can’t be reversed. We won’t go to the mechanics of the functions themselves — there are plenty of great articles that cover that. Instead, we will look at how using these functions in the correct order can lead you to the Bitcoin wallet address that you can use.

Elliptic Curve Cryptography

The first thing we need to do is to apply the ECDSA or Elliptic Curve Digital Signature Algorithm to our private key. An elliptic curve is a curve defined by the equation y² = x³ + ax + b with a chosen a and b. There is a whole family of such curves that are widely known and used. Bitcoin uses the secp256k1 curve. If you want to learn more about Elliptic Curve Cryptography, I’ll refer you to this article.

By applying the ECDSA to the private key, we get a 64-byte integer. This consists of two 32-byte integers that represent the X and Y of the point on the elliptic curve, concatenated together.

For our example, we got: 1e7bcc70c72770dbb72fea022e8a6d07f814d2ebe4de9ae3f7af75bf706902a7b73ff919898c836396a6b0c96812c3213b99372050853bd1678da0ead14487d7.

In Python, it would look like this:

Note: as you can see from the code, before I used a method from the ecdsa module, I decoded the private key using codecs. This is relevant more to the Python and less to the algorithm itself, but I will explain what are we doing here to remove possible confusion.

In Python, there are at least two classes that can keep the private and public keys: “str” and “bytes”. The first is a string and the second is a byte array. Cryptographic methods in Python work with a “bytes” class, taking it as input and returning it as the result. Command to generate ssh key in hadoop.

Now, there’s a little catch: a string, say, 4f3c does not equal the byte array 4f3c, it equals the byte array with two elements, O&lt;. And that’s what codecs.decode method does: it converts a string into a byte array. That will be the same for all cryptographic manipulations that we’ll do in this article.

Public key

Once we’re done with the ECDSA, all we need to do is to add the bytes 0x04 at the start of our public key. The result is a Bitcoin full public key, which is equal to: 041e7bcc70c72770dbb72fea022e8a6d07f814d2ebe4de9ae3f7af75bf706902a7b73ff919898c836396a6b0c96812c3213b99372050853bd1678da0ead14487d7 for us.

Compressed public key

Python Generate Private Key Bitcoin Online

But we can do better. As you might remember, the public key is some point (X, Y) on the curve. We know the curve, and for each X there are only two Ys that define the point which lies on that curve. So why keep Y? Instead, let’s keep X and the sign of Y. Later, we can derive Y from that if needed.

The specifics are as follows: we take X from the ECDSA public key. Now, we add the 0x02 if the last byte of Y is even, and the byte 0x03 if the last byte is odd.

In our case, the last byte is odd, so we add 0x03 to get the compressed public key: 031e7bcc70c72770dbb72fea022e8a6d07f814d2ebe4de9ae3f7af75bf706902a7. This key contains the same information, but it’s almost twice as short as the uncompressed key. Cool!

Previously, wallet software used long, full versions of public keys, but now most of it has switched to compressed keys.

Encrypting the public key

From now on, we need to make a wallet address. Whatever method of getting the public key you choose, it goes through the same procedure. Obviously, the addresses will differ. In this article, we will go with the compressed version.

What we need to do here is to apply SHA-256 to the public key, and then apply RIPEMD-160 to the result. The order is important.

SHA-256 and RIPEMD-160 are two hash functions, and again, we won’t go into the details of how they work. What matters is that now we have 160-bit integer, which will be used for further modifications. Let’s call that an encrypted public key. For our example, the encrypted public key is 453233600a96384bb8d73d400984117ac84d7e8b.

Here’s how we encrypt the public key in Python:

Adding the network byte

The Bitcoin has two networks, main and test. The main network is the network that all people use to transfer the coins. The test network was created — you guessed it — to test new features and software.

We want to generate an address to use it on the mainnet, so we need to add 0x00 bytes to the encrypted public key. The result is 00453233600a96384bb8d73d400984117ac84d7e8b. For the testnet, that would be 0x6f bytes.

Checksum

Now we need to calculate the checksum of our mainnet key. The idea of checksum is to make sure that the data (in our case, the key) wasn’t corrupted during transmission. The wallet software should look at the checksum and mark the address as invalid if the checksum mismatches.

To calculate the checksum of the key, we need to apply SHA-256 twice and then take first 4 bytes of the result. For our example, the double SHA-256 is 512f43c48517a75e58a7ec4c554ecd1a8f9603c891b46325006abf39c5c6b995 and therefore the checksum is 512f43c4 (note that 4 bytes is 8 hex digits).

The code to calculate an address checksum is the following:

Getting the address

Finally, to make an address, we just concatenate the mainnet key and the checksum. That makes it 00453233600a96384bb8d73d400984117ac84d7e8b512f43c4 for our example.

That’s it! That’s the wallet address for the private key at the start of the article.

But you may notice that something is off. You’ve probably seen a handful of Bitcoin addresses and they didn’t look like that. Well, the reason is that they are encoded with Base58. It’s a little bit odd.

Here’s the algorithm to convert a hex address to the Base58 address:

What we get is 17JsmEygbbEUEpvt4PFtYaTeSqfb9ki1F1, a compressed Bitcoin wallet address.

Conclusion

The wallet key generation process can be split into four steps:

• creating a public key with ECDSA
• encrypting the key with SHA-256 and RIPEMD-160
• calculating the checksum with double SHA-256
• encoding the key with Base58.

Depending on the form of public key (full or compressed), we get different addresses, but both are perfectly valid.

Here’s the full algorithm for the uncompressed public key:

If you want to play with the code, I published it to the Github repository.

I am making a course on cryptocurrencies here on freeCodeCamp News. The first part is a detailed description of the blockchain.

I also post random thoughts about crypto on Twitter, so you might want to check it out.

This page contains sample addresses and/or private keys. Do not send bitcoins to or import any sample keys; you will lose your money.

A private key in the context of Bitcoin is a secret number that allows bitcoins to be spent.Every Bitcoin wallet contains one or more private keys, which are saved in the wallet file.The private keys are mathematically related to all Bitcoin addresses generated for the wallet.

Because the private key is the 'ticket' that allows someone to spend bitcoins, it is important that these are kept secret and safe.Private keys can be kept on computer files, but are also often written on paper.

Private keys themselves are almost never handled by the user, instead the user will typically be given a seed phrase that encodes the same information as private keys.

Some wallets allow private keys to be imported without generating any transactions while other wallets or services require that the private key be swept.When a private key is swept, a transaction is broadcast that sends the balance controlled by the private key to a new address in the wallet.Just as with any other transaction, there is risk of swept transactions to be double-spending.

In contrast, bitcoind provides a facility to import a private key without creating a sweep transaction.This is considered very dangerous, and not intended to be used even by power users or experts except in very specific cases. Importing keys could lead to the Bitcoins being stolen at any time, from a wallet which has imported an untrusted or otherwise insecure private key - this can include private keys generated offline and never seen by someone else^[1][2].

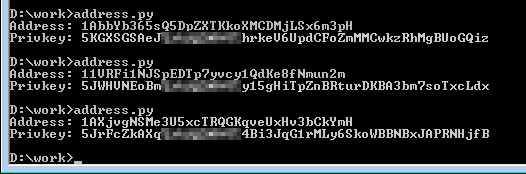
An example private key

In Bitcoin, a private key is a 256-bit number, which can be represented one of several ways.Here is a private key in hexadecimal - 256 bits in hexadecimal is 32 bytes, or 64 characters in the range 0-9 or A-F.

Range of valid ECDSA private keys

Nearly every 256-bit number is a valid ECDSA private key. Specifically, any 256-bit number from 0x1 to 0xFFFF FFFF FFFF FFFF FFFF FFFF FFFF FFFE BAAE DCE6 AF48 A03B BFD2 5E8C D036 4140 is a valid private key.

The range of valid private keys is governed by the secp256k1 ECDSA standard used by Bitcoin.

Hierarchical Deterministic (HD) Wallet Keys

Main article: Hierarchical deterministic wallet

Wallet software may use a BIP 32 seed to generate many private keys and corresponding public keys from a single secret value. This is called a hierarchical deterministic wallet, or HD wallet for short. The seed value, or master extended key, consists of a 256-bit private key and a 256-bit chain code, for 512 bits in total. The seed value should not be confused with the private keys used directly to sign Bitcoin transactions.

Users are strongly advised to use HD wallets, for safety reasons: An HD wallet only needs to be backed up once typically using a seed phrase; thereafter in the future, that single backup can always deterministically regenerate the same private keys. Therefore, it can safely recover all addresses, and all funds sent to those addresses. Non-HD wallets generate a new randomly-selected private key for each new address; therefore, if the wallet file is lost or damaged, the user will irretrievably lose all funds received to addresses generated after the most recent backup.

Base58 Wallet Import format

Main article: Wallet import format

When importing or sweeping ECDSA private keys, a shorter format known as wallet import format is often used, which offers a few advantages.The wallet import format is shorter, and includes built-in error checking codes so that typos can be automatically detected and/or corrected (which is impossible in hex format) and type bits indicating how it is intended to be used.Wallet import format is the most common way to represent private keys in Bitcoin.For private keys associated with uncompressed public keys, they are 51 characters and always start with the number 5 on mainnet (9 on testnet). Private keys associated with compressed public keys are 52 characters and start with a capital L or K on mainnet (c on testnet). This is the same private key in (mainnet) wallet import format:

When a WIF private key is imported, it always corresponds to exactly one Bitcoin address.Any utility which performs the conversion can display the matching Bitcoin address.The mathematical conversion is somewhat complex and best left to a computer, but it's notable that the WIF guarantees it will always correspond to the same address no matter which program is used to convert it.

The Bitcoin address implemented using the sample above is: 1CC3X2gu58d6wXUW_SAMPLE_ADDRESS_DO_NOT_SEND_MffpuzN9JAfTUWu4Kj

Python Generate Private Key Bitcoin Account

Mini private key format

Main article: Mini private key format

Some applications use the mini private key format. Not every private key or Bitcoin address has a corresponding mini private key - they have to be generated a certain way in order to ensure a mini private key exists for an address. The mini private key is used for applications where space is critical, such as in QR codes and in physical bitcoins. The above example has a mini key, which is:

Summary

Python Generate Public Key From Private Key Bitcoin

Any Bitcoins sent to the address 1CC3X2gu58d6wXUW_SAMPLE_ADDRESS_DO_NOT_SEND_MffpuzN9JAfTUWu4Kj can be spent by anybody who knows the private key implementing it in any of the three formats, regardless of when the bitcoins were sent, unless the wallet receiving them has since made use of the coins generated.The private key is only needed to spend the bitcoins, not necessarily to see the value of them.

If a private key controlling unspent bitcoins is compromised or stolen, the value can only be protected if it is immediately spent to a different output which is secure.Because bitcoins can only be spent once, when they are spent using a private key, the private key becomes worthless.It is often possible, but inadvisable and insecure, to use the address implemented by the private key again, in which case the same private key would be reused.

See Also

References

1. ↑Bitcoin StackExchange - Why doc says importing private keys is so dangerous?
2. ↑Bitcoin StackExchange - Why so many warnings about importing private keys?